参考资料：

理解

  • 建立时间就是时钟触发事件来临之前，数据需要保持稳定的最小时间，以便数据能够被时钟正确的采样。
  • 保持时间就是时钟触发事件来临之后，数据需要保持稳定的最小时间，以便数据能够被电路准确的传输。

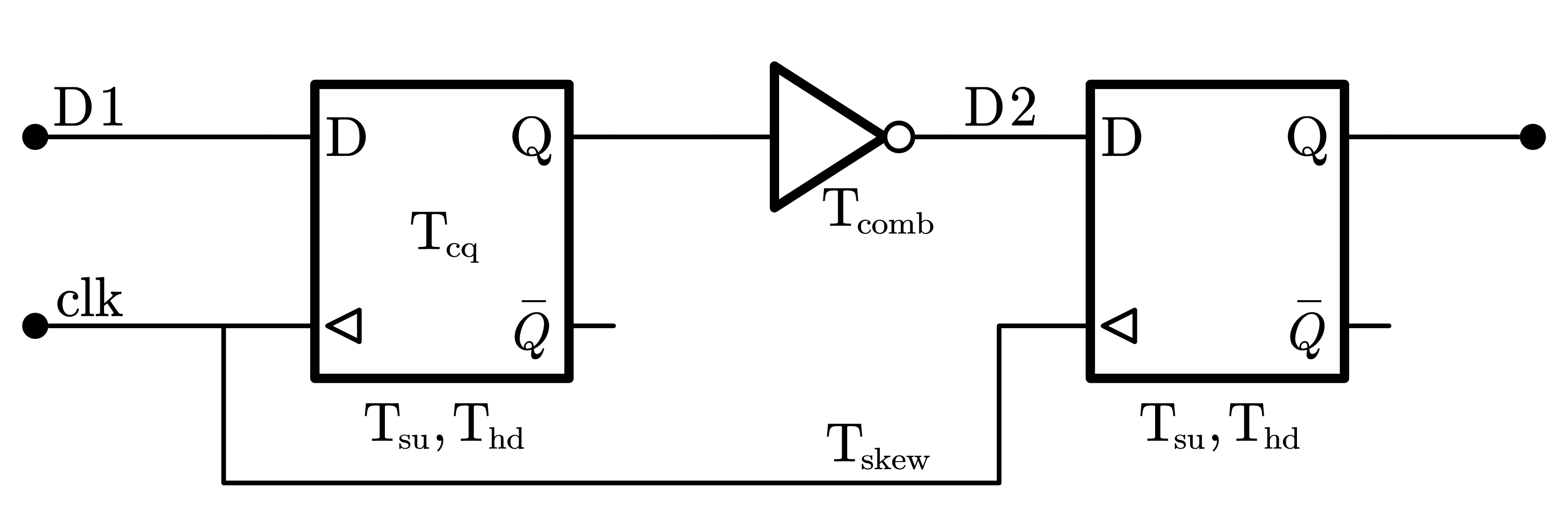
数字电路.png

Thd≤Tcq−Tskew+TcombTsu≤Tclk−T^hd\begin{aligned}
T_{hd}&\leq T_{cq}-T_{skew}+T_{comb} \
T_{su}&\leq T_{clk}-\hat{T}_{hd}
\end{aligned}
Thd​Tsu​​≤Tcq​−Tskew​+Tcomb​≤Tclk​−T^hd​​

建立时间保持时间

1
2
3
4
5
6
7
8
9
10
{ signal: [
  { name: "clk",      wave: "p..", node:'.ab'},
  { name: "D1",       wave: "01.", phase: 0.5},
  { name: "Q1",       wave: "01." ,phase:-1, node:'.c'},
  { name: "clk_skew", wave: "p..", node:'.de', phase:-0.8},
  { name: "D2",       wave: "01.", phase:-3, node:'.f'},
  ],
  config: { hscale: 5 },
  edge: ['a-b Tclk', 'a-~c Tcq', 'c-~f Tcomb', 'a~-d Tskew','b-~e Tskew', 'd~-f >Thd', 'f-~e >Tsu']
}

例题

例1：考虑线网延迟，某电路各种延迟值（单位：ns）如下，时钟周期为 15ns，请判断该电路的建立时间和保持时间是否存在 violation ？

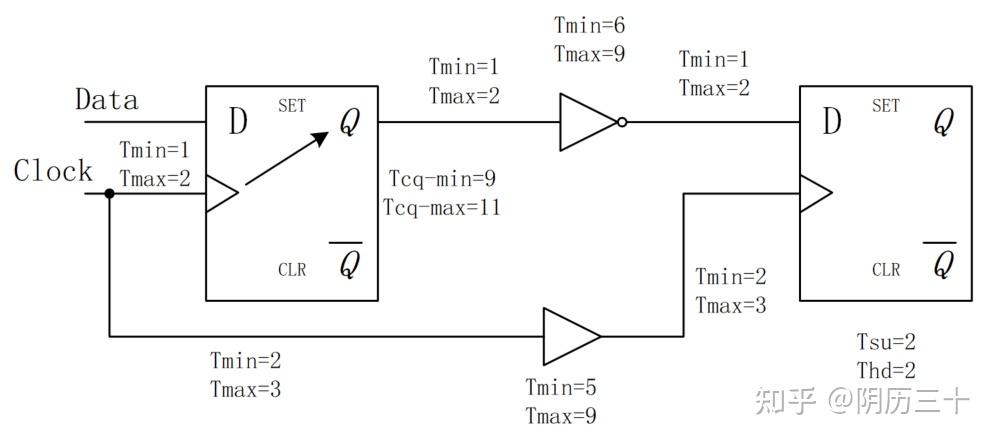
答案：保持时间裕量为 1 ；建立时间 violation，裕量为 -4；

Thd≤min⁡(Tcq+Tcomp)−max⁡(Tskew)T_{hd} \leq \min(T_{cq}+T_{comp})-\max(T_{skew})Thd​≤min(Tcq​+Tcomp​)−max(Tskew​)

Tsu≤Tck−max⁡(Tcq+Tcomp)+min⁡(Tskew)T_{su} \leq T_{ck} - \max(T_{cq}+T_{comp})+\min(T_{skew})Tsu​≤Tck​−max(Tcq​+Tcomp​)+min(Tskew​)

例2： 一道知名公司的面试题：时钟周期为 T, 第一级触发器 D1 建立时间最大值为 T1max，最小值为 T1min。组合逻辑最大延迟为 T2max, 最小值为 T2min。问：第二级触发器 D2 的建立时间和保持时间应该满足什么条件？

答案：

第二级触发器的建立时间与保持时间与第一级的触发器没有直接关系；

列出约束关系，并根据已知参数适当取舍，得到简化后的约束关系如下：

Thd≤T2minTsu≤T−T2max\begin{aligned}
T_{hd}&\leq T_{2min} \
T_{su}&\leq T-T_{2max}
\end{aligned}
Thd​Tsu​​≤T2min​≤T−T2max​​

例3：一种简单的分频电路如下所示。该触发器建立时间为 3ns, 保持时间为 3ns， 逻辑延迟为 6ns，两个反相器延迟为 1ns，连线延迟为 0。则该电路的最高工作频率是多少？

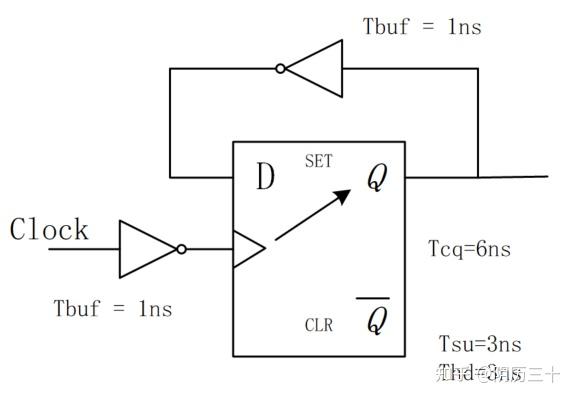
答案：

只有一个时钟，一个触发器，没有时钟偏移，clock path 的反相器延迟是迷惑项。

最高工作频率为 100MHz

例4：

（1）以下电路固有的建立时间和保持时间？

（2）该电路最高的工作频率？

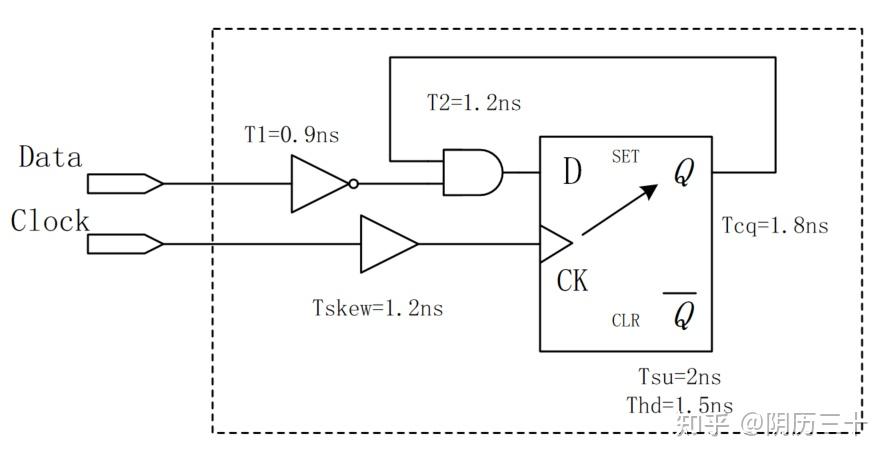
1
2
3
4
5
6
7
8
9
10
11
12
13
14
{ signal: [
  { name: "Clock",    wave: "P...",node: '.ah', phase: 0.8, period:2},
  {},
  { name: "Data",     wave: "====",node: '.d.e', phase: 3.7, period: 2},
  {},
  { name: "CK",       wave: "P..", node: '.bg', period: 2 },
  {},
  { name: "D",        wave: "====",node: '.c.f', phase: 2.15, period: 2},
  ],
  config: { hscale: 2 },
  edge: ['b~-a Tskew', 'c-~d Tcomb', 'b~-c Tsu', 'a-~d 固有建立时间',
         'g~-f Thd', 'h-~e 固有保持时间', 'e-~f Tcomb', 'h~-g Tskew'
  ]
}

答案：

该电路固有的建立时间为：2.1 + 2 - 1.2 = 2.9ns

固有的保持时间为：1.2 + 1.5 - 2.1 = 0.6ns

此电路仍然是自身到自身的反馈电路。所以没有时钟偏移，也无需考虑 T1 = 0.9ns 的延迟。所以最高工作频率为： 1 / (1.8 + 1.2 + 2)ns = 200MHz